支持向量机
[toc]
数学基础补充
二元函数的无条件极值问题
- 求偏导等于0,找到所有驻点(必要条件)
- 求二阶偏导,依次确定各驻点处A、B、C的值,根据$$AC-B^2$$的符号判断是否为极值点(充分条件)
- 大于0,有极值。A>0极小值,反之极大值
- 小于0,没有极值
- 等于0,可能有也可能没有
这通常对应一个最简单的无约束优化问题
条件极值和拉格朗日乘数法
条件极值:对自变量有附加条件的极值
设二元函数$$f(x,y)$$和$$\phi(x,y)$$在区域D内有一阶连续偏导数,则求$$z = f(x,y)$$在D内满足条件$$\phi(x,y)$$的极值问题,可以转化为求拉格朗日函数
$$
L(x,y,\lambda) = f(x,y) + \lambda\phi(x,y)~~~~~ (其中\lambda是某一常数)
$$
的无条件极值问题
其中我们称一维向量$$\lambda_i$$是一个拉格朗日乘子
这通常用于求解带有等式约束的优化问题
数学符号说明
最大最小
$$
g(\lambda) = max_{x \in D}f(x,\lambda)
$$
- 这是一个关于$$\lambda$$的函数
- 当 $$\lambda = y$$ 时,$$g(\lambda)$$ 的取值为: 固定 $$f(x,\lambda)$$ 中的 $$\lambda = y $$ ,变动 x 时 f 能娶到的最大值
$$
g(\lambda) = max_\lambda ~min_x ~f(x,\lambda)
$$
- 从右往左看,首先把min这一项看作关于$$\lambda$$ 的函数$$g(\lambda)$$ ,然后求这个函数的最大值
inf和sup符号
inf 是下确界,sup 上确界。和最大最小值相似但不同,max f 不存在的情况下 sup f 可能存在
凸函数凹函数
使用国内定义还是国际定义仁者见仁智者见智了(以下使用国际定义)
但是要记得詹森不等式
$$
凸函数:和的函数值 \le 函数值的和 \
凹函数:和的函数值 \ge 函数值的和
$$
仿射函数是又凹又凸的
max是凹函数、min是凸函数(利用詹森不等式证明)
拉格朗日对偶问题
原问题
$$
\begin{aligned}
\min_{\mathbf{x}\in \mathbb{R} ^{\mathtt{n}}} \mathbf{f}\left( \mathbf{x} \right)\
\mathbf{s}.\mathbf{t}\quad \mathbf{c}{\mathtt{i}}\left( \mathbf{x} \right) &\leqslant \mathbf{0},\mathbf{i}\in \left[ \mathtt{1},\mathtt{k} \right]\
\quad \quad \mathtt{h}{\mathtt{j}}\left( \mathbf{x} \right) &=\mathbf{0},\mathbf{j}\in \left[ \mathtt{1},\mathbf{l} \right]\
\end{aligned}
$$
凸优化 要求$$f(x)$$ 是凸函数, $$c_i(x)$$ 是凸函数, $$h_j(x)$$ 是仿射函数
但这里我们做两个约定
- 我们不假定原函数 f 的凹凸性, f 既可以是凹函数也可以是凸函数
- 问题的定义域 $$\mathrm{D}=(\mathrm{dom} \mathrm{f)}\cap (\bigcap\nolimits_{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{c}{\mathrm{i}})}\cap (\bigcap\nolimits{\mathrm{i}=1}^{\mathrm{l}}{\mathrm{h}_{\mathrm{i}})}$$
- D 不是 空集
- 我们约定最终求出来的最优结果用$$p^*$$表示
对偶问题
定义:实质相同但从不同角度提出不同提法的一对问题。
在原问题中, 约束条件太多,并且凹凸性不明确。 于是我们将他转化为拉格朗日对偶问题。这样的有点是:只有一个约束,并且拉格朗日对偶问题一定是凹的。
证明如下:
- 类比于等式约束的最值问题,我们为原问题构建一个广义拉格朗日函数
$$
\begin{aligned}
\mathcal{L} :\mathbb{R} ^{\mathtt{n}}\times \mathbb{R} ^{\Bbbk}\times \mathbb{R} ^{\mathrm{l}}\rightarrow \mathrm{R}\
\mathcal{L} (\mathtt{x},\mathrm{\lambda},\mathrm{\mu)}&=\mathtt{f}(\mathtt{x})+\sum_{\mathrm{i}=1}^{\mathrm{k}}{\lambda {\mathrm{i}}\mathrm{c}{\mathrm{i}}(\mathtt{x})}+\sum_{\mathrm{j}=1}^{\mathrm{l}}{\mathrm{\mu}{\mathrm{j}}\mathrm{h}{\mathrm{j}}(\mathtt{x})}\
\vec{\mathtt{x}}\in \mathbb{R} ^{\mathtt{n}},\vec{\lambda}\in \mathbb{R} ^{\Bbbk},\vec{\mathrm{\mu}}\in \mathbb{R} ^{\mathrm{l}}\
\end{aligned}
$$
- 根据 L 我们定义一个拉格朗日对偶函数 g(lambda, mu)
$$
\begin{aligned}
\mathtt{g}(\mathrm{\lambda},\mathrm{\mu)}&=\mathop {\mathrm{inf}} \limits_{\mathtt{x}\in \mathrm{D}}\mathcal{L} (\mathtt{x},\mathrm{\lambda},\mathrm{\mu)}\
&=\mathop {\mathrm{inf}} \limits_{\mathtt{x}\in \mathrm{D}}\bigl( \mathtt{f}(\mathtt{x})+\sum_{\mathtt{i}=\mathtt{l}}^{\mathtt{k}}{\lambda {\mathtt{i}}\mathrm{c}{\mathtt{i}}(\mathtt{x})}+\sum_{\mathtt{j}=\mathtt{l}}^{\mathtt{l}}{\mathrm{\mu}{\mathtt{j}}\mathrm{h}{\mathtt{j}}(\mathtt{x})} \bigr)\
\lambda &\geqslant 0\
\end{aligned}
$$
可以证明这个函数一定是凹函数。
我们总结得到:不管原函数 f 的凹凸性, 它的对偶函数 g 一定是凹函数
我们之所以需要这么一个对偶函数是因为只要 λ 不小于 0 , g的值永远不会超过 $$p^*$$。证明略
也就是说, $$p^*$$永远都不会小于 $$max~g(\lambda,\mu)$$
从原问题到拉格朗日对偶问题
我们通过拉格朗日对偶函数给出了最优解 $$p^$$的下界,也就是说我们通过求$$max~g(\lambda,\mu)$$来逼近$$p^$$的值
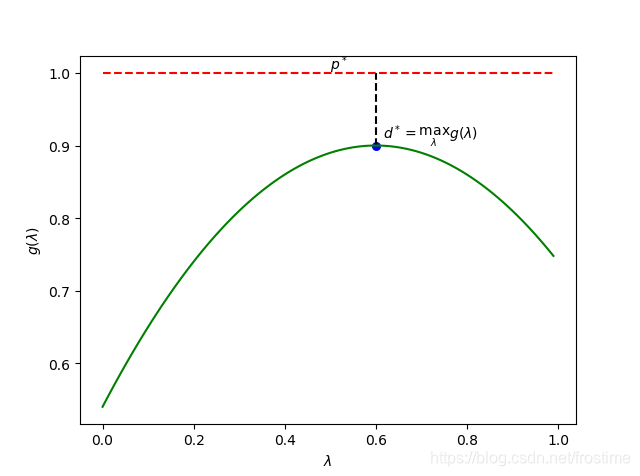
回顾原问题,我们现在给出对偶问题的形式
$$
\begin{aligned}
\max_{\lambda ,\mu} \mathtt{g}(\lambda ,\mu )&=\max_{\lambda ,\mu} \mathop {\mathrm{inf}} \limits_{\mathtt{x}\in \mathrm{D}}\mathcal{L} (\mathtt{x},\lambda ,\mu )\
\mathrm{s}.\mathrm{t}\quad \lambda _{\mathtt{i}}&\geqslant \mathtt{0},\mathtt{i}=\mathtt{1},\mathtt{2},…,\mathtt{k}\
\end{aligned}
$$
这是个凸优化问题,我们转而去求 d^* 了。
KKT条件
学习中……
基础概念
超平面
二维空间上,两类点被一条直线完全分开叫做线性可分
拓展到n维空间上,将n维欧氏空间上的两个点集$$D_1$$ 和$$D_2$$完全正确地划分开的 $$wx + b = 0$$就成了一个超平面。
支持向量
样本中距离超平面最近的一些点叫做支持向量
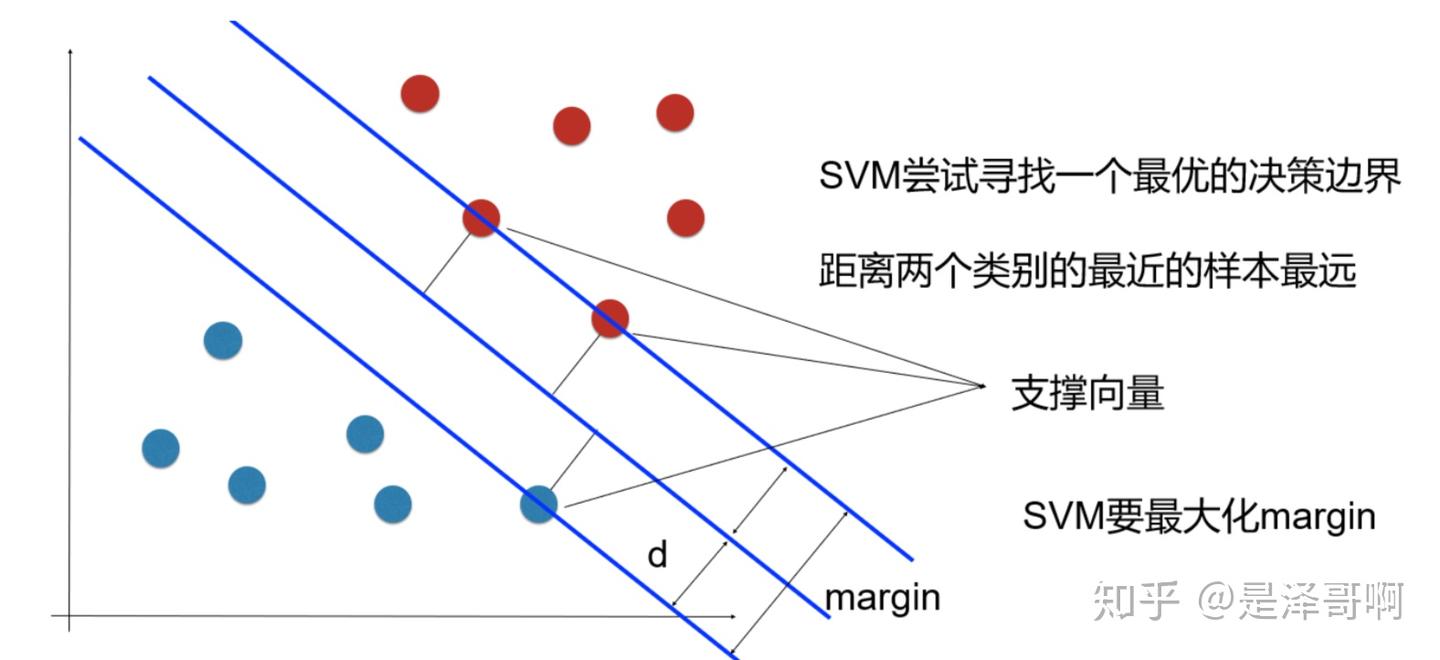
SVM最优化问题
SVM想要找到的就是 最大间隔超平面,即支持向量离超平面最远
任意超平面可以用以下线性方程来描述:
$$
w^T x + b = 0
$$
由点到直线的距离公式推导可得,n维向量到超平面的距离为:
$$
\frac{|w^T x + b = 0|}{||w||}
$$
其中 $$||w||$$ = $$\sqrt{w_1^2+…+w_n^2}$$
我们假设支持向量到超平面的距离为 d,可知其他向量到超平面的距离 > d,于是我们可以这样描述超平面两端的向量:
$$
\left{ \begin{aligned}
\frac{\boldsymbol{w}^T\boldsymbol{x}+\boldsymbol{b}}{||\boldsymbol{w}||}&\ge \boldsymbol{d}\quad \boldsymbol{y}=\boldsymbol{1}\
\frac{\boldsymbol{w}^T\boldsymbol{x}+\boldsymbol{b}}{||\boldsymbol{w}||}&\le -\boldsymbol{d}\quad \boldsymbol{y}=-\boldsymbol{1}\
\end{aligned} \right.
$$
由于 $$||w||d$$ 严格大于0,我们假设它为 1