计算器原理

计算器计算的表达式是后缀表达式。

我们输入一个表达式，计算器给出结果主要经过了：将中缀表达式转化为后缀表达式，计算后缀表达式这两个过程

而转化和计算过程运用到了数据结构“栈”。

我们为了简化过程，在转化后缀表达式过程中进行中间结果的计算。

中缀表达式

中缀表示法 - 维基百科，自由的百科全书

中缀表达法是自然语言的写法，其操作符在操作数的中间

如3+4

后缀表达式（逆波兰表示法）

逆波兰表示法 - 维基百科，自由的百科全书

即所有操作符在操作数的后面。

求值过程

1. 从左到右扫描表达式
2. 遇到数字时，将数字压入堆栈
3. 遇到运算符时
   • 弹出栈顶的两个数（栈顶和次顶），用运算符对它们做对应的计算，并将结果入栈
   • 计算顺序是： 后弹出来的 （运算符） 先弹出来的

调度场算法

调度场算法 - 维基百科，自由的百科全书

将中缀表达式转化为后缀表达式的算法。

为了方便快速计算，我们使用两个栈：运算符栈s1和操作数栈s2。操作数栈其实也可以看作中间结果栈。

在操作数压栈过程中，直接入栈即可。

在运算符压栈过程中，需要保持栈顶运算符为当前优先级最高的。换言之就是比当前栈内运算符优先级高的运算符已经完成了运算操作。

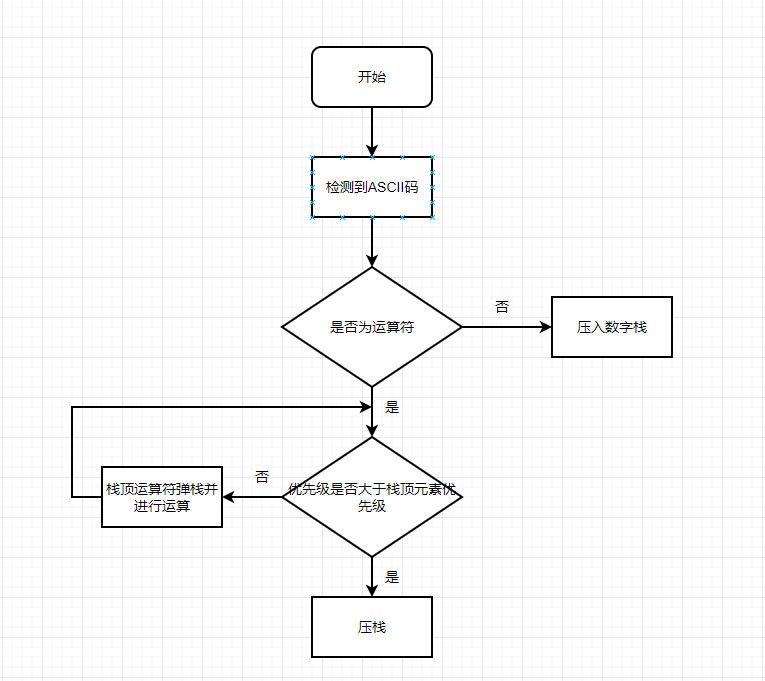
详细步骤：

1. 初始化两个栈：

   • 运算符栈：s1
   • 中间结果栈：s2

2. 从左到右扫描中缀表达式

3. 遇到操作数时，将其压入s2

4. 遇到运算符时

   • 比较它和s1栈顶运算符的优先级：
     • 如果s1为空或者栈顶运算符符号为（，则将其压入符号栈s1
     • 如果优先级比栈顶运算符高，也将其压入符号栈s1
     • 如果优先级比栈顶运算符低或相等，将s1栈顶的运算符弹出，并压入到s2中。
   • 再重复比较它和新栈顶运算符的优先级。

   [!NOTE]

   重复的含义：

   1. 如果s1栈顶元素符号优先级比当前符号高或者等于，那么就将其弹出压入s2中（循环做，只要s1不为空）。

      如果栈顶符号为 （ ，其优先级最低，就不会弹出，就跳出循环了。

   2. 跳出循环后，则将当前符号压入s1

5. 遇到括号时：

   • 如果是左括号（ ：则直接压入s1
   • 如果是右括号 ）：则以此弹出s1栈顶的运算符，并压入s2，知道遇到左括号为止，此时将这一对括号丢弃。

6. 重复步骤2~5，直到表达式最右端。

7. 将s1中的运算符以此弹出并压入 s2。

8. 以此弹出 s2 中的元素并输出，结果的 逆序 即为：中缀表达式转为后缀表达式。

举例：

1+((2+3)*4)-5	

扫描到的元素	s2(栈底->栈顶)	s1(栈底->栈顶)	说明
1	4	空	遇到操作数，压入s2
+	1	+	s1栈为空，压入s1
（	1	+（	左括号，压入s1
（	1	+（（	左括号，压入s1
2	1 2	+（（	遇到操作数，压入s2
+	1 2	+（（+	栈顶为（，压入s2
3	1 2 3	+（（+	遇到操作数，压入s2
）	1 2 3 +	+（	遇到右括号，弹出+后遇到左括号，删除一对小括号
*	1 2 3 +	+（*	遇到操作符，压入s1
4	1 2 3 + 4	+（*	遇到操作数，压入s2
）	1 2 3 + 4 *	+	遇到右括号，弹出*后遇到左括号，删除一对小括号
-	1 2 3 + 4 * +	-	遇到操作符，优先级相等，弹出+后s1为空，此时将-压入 s1
5	1 2 3 + 4 * + 5	-	遇到操作数，压入s2
null	1 2 3 + 4 * + 5 -	空	解析完毕，弹出s1中符号并压入s2中

结果：1 2 3 + 4 * + 5

这是理论上转化后缀码的步骤。

优化后的程序为

扫描到的元素	s2(栈底->栈顶)	s1（栈底->栈顶）	说明
1	4	空
+	1	+
（	1	+（（
2	1 2	+（（
+	1 2	+（（+
3	1 2 3	+（（+
）	1 5	+（	将+压入s1，消除小括号，s2计算3 + 2
*	1 5	+（*
4	1 5 4	+（*
）	1 20	+	将*压入s1，消除小括号，是、s2计算 4 * 5
-	21	-	将+压入s2，计算20+1
5	21 5	-
null	16		将s1弹栈，压入s2

结果为16

这个讲数据结构的笔记挺好的： 数据结构与算法 系列教程（笔记）